几何问题中经常会遇到求长度、面积、体积的题目,如果图形规则,可以直接套用公式,但若图形不规则,或者虽然规则但是不能直接套用公式的话,此时需要用到割补平移的方式将图形转换成我们知道的形式,进而求解题目。本文在这里通过例题讲解帮助考试发散思维,培养利用割补平移思考问题解决问题的能力。
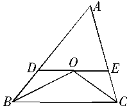
【例题1】: 如右图所示,△ABC中DE∥BC,且BO和CO分别是∠ABC和∠ACB的角平分线。已知AB=25.4cm,BC=24.5cm,AC=20cm。问△ADE的周长是多少?
A.45.4cm
B.45.1cm
C.44.8cm
D.44.5cm
【参考答案】:A。
【解析】:平移法。已知DE与BC平行,所以∠DOB=∠OBC,∠EOC=∠OCB。又因为BO和CO分别是∠ABC和∠ACB的角平分线,所以∠DBO=∠OBC=∠DOB,∠ECO=∠OCB=∠EOC。因此,△DBO与△EOC均为等腰三角形,BD=DO,OE=EC,△ADE的周长就等于AD+DE+AE=AD+DO+AE+EO=AD+DB+AE+EC=AB+AC=25.4+20=45.4cm。
【小结】:此题要求规则图形的周长,但是没法套用公式直接求解,利用角平分线等性质将所求的线段长度进行替换,转化为已知线段的长度进而求解。
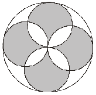
【例题2】: 在下图中,大圆的半径是8,求阴影部分的面积是多少?
A.120
B.128
C.136
D.144
【参考答案】:B。
【解析】:割补法。阴影部分可拼成一个对角线长为16的正方形。如图,故面积是16×16÷2=128。
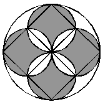
【小结】:此题要求不规则几何图形的面积,我们可以利用割补法,将其转化为规则几何图形的面积,这样能够大大节省解题的步骤。

